가격에 따라 판매량이 결정되는 그래프가 f(x)가 다음과 같다고 하자
$$f(x) = -x^3 + 2\ \ \ (0 ≤ x ≤2^{\frac{1}{3}})$$
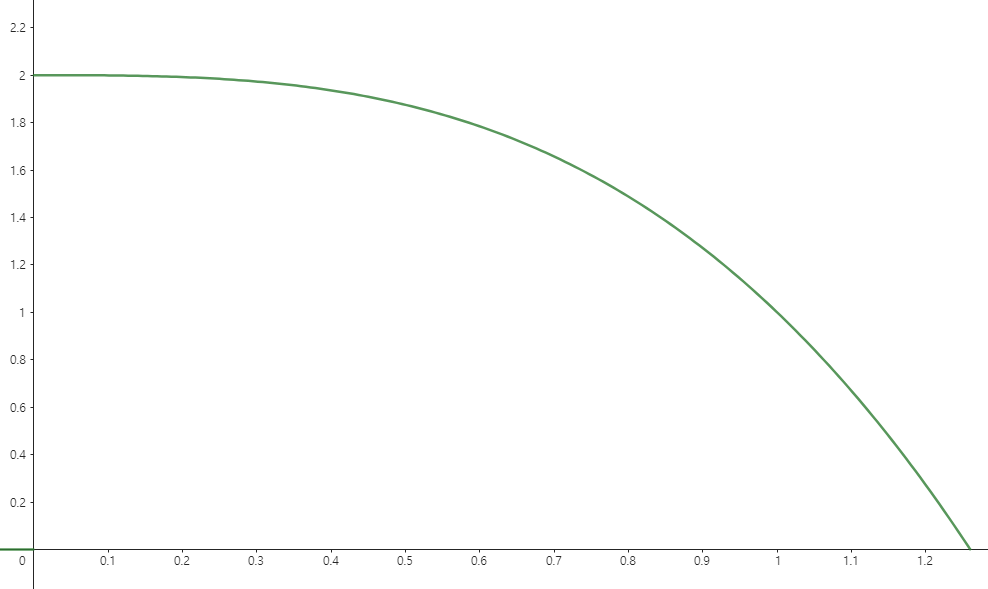
판매량은 f(x)이고, 가격은 x임이 분명하므로 판매수익은 x * f(x)이다.
$$xf(x) = -x^4+2x\ \ \ (0 ≤ x ≤2^{\frac{1}{3}})$$

판매수익이 최대인 곳은 그래프의 가장 높은 곳이다.
즉 판매수익이 최대인 위치가 이번에 배울 극댓값이자 최댓값인 것이다.
이제 극댓값과 최댓값이 무엇인지 알아보자
- 최댓값과 최솟값 / 극값
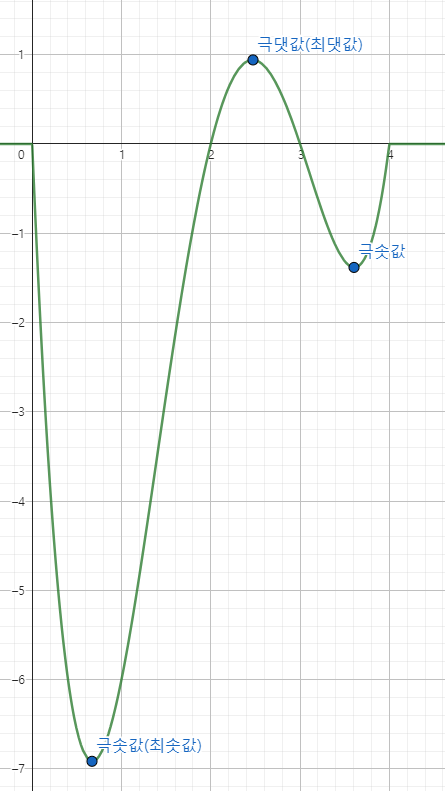
위 그래프를 통해 최솟값은 주어진 범위에서 가장 작은 값이고
최댓값은 주어진 범위에서 가장 큰 값임을 알 수 있다.
그렇다면 극값은 어떻게 정해지는 것일까?
극솟값이자 최솟값인 점의 x값을 a라고 하자.
a의 주변에서의 x에 대한 함숫값 f(x) 값이 f(a) ≤ f(x)를 만족할 때 극소라고 하고
최댓값인 점의 x값을 b라고 하였을 때
b의 주변에서의 x에 대한 함수값 f(x)값이 f(b) ≥ f(x)를 만족할때 극대라고 한다.
- 임계수
임계수란 f'(c) = 0이거나 f'(c)가 존재하지 않는 f의 정의역에 속한 수 c를 말한다.
예제 1.
$$함수\ f(x) = X^3-x^2의\ 임계수를\ 구하라.$$
풀이 1.
$$f의\ 도함수는\ f'(x) = 3x^2-2x이다.\ 모든\ 실수\ x에\ 대하여\ f'(x)가\ 존재하므로$$
$$임계수는\ f'(x) = 0인\ 경우에만\ 나타난다.$$
$$즉\ 3x(x-\frac{2}{3}) = 0의\ 해가\ 임계수가\ 된다.$$
$$∴\ x = 0\ 또는\ x = \frac{2}{3}$$
'CALCULUS 핵심미분적분학' 카테고리의 다른 글
| CALCULUS 핵심 미적분학 (제 9판) |4 - 1 - (2)평균값 정리 (1) | 2024.10.13 |
|---|---|
| CALCULUS 핵심 미적분학 (제 9판) | 3 - 5 쌍곡선함수 (1) | 2024.10.11 |
| CALCULUS 핵심 미적분학 (제 9판) | 3 - 4 선형 근사 (8) | 2024.10.11 |
| CALCULUS 핵심 미적분학 (제 9판) | 로그함수와 역삼각함수의 도함수 (1) | 2024.10.10 |
| CALCULUS 핵심 미적분학 (제 9판) | 3 - 2 음함수 미분법 (1) | 2024.10.10 |


